在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变，纵坐标扩大到原来的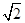
倍后得到点Q(x,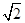y),且满足
·
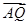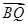=1.
(Ⅰ)求动点P所在曲线C的方程；
(Ⅱ)过点B作斜率为-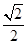
的直线l交曲线C于M、N两点，且
+
+
=
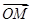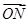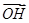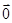，试求△MNH的面积.
相关试题
．
的最大值；
，求证：
；
时，
成立，求实数
的最小值．
．
的单调性；
恒成立，求
的范围．
．
是等比数列，并求数列
的通项公式；
，求和
，并证明：
．
中，
，
．
平面
；
与平面
．
；
的解集．推荐套卷
在平面直角坐标系内已知两点A(-1,0)、B(1,0),若将动点P(x,y)的横坐标保持不变，纵坐标扩大到原来的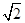倍后得到点Q(x,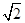y),且满足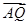·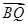=1.
(Ⅰ)求动点P所在曲线C的方程；
(Ⅱ)过点B作斜率为-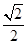的直线l交曲线C于M、N两点，且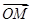++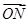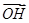=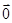，试求△MNH的面积.
粤公网安备 44130202000953号