)如图,在正三棱柱ABC—A1B1C1中,AB=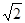 AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。
推荐套卷
)如图,在正三棱柱ABC—A1B1C1中,AB=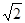 AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
AA1,点D是A1B1的中点,点F是AB的中点,点E在A1C1上,且DE⊥AE。
(1)证明B1F//平面ADE;
(2)证明平面ABC1⊥平面C1DF;
(3)求直线AD和平面ABC1所成角的正弦值。