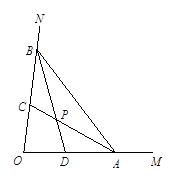（1）如图，∠MON＝80º，点A、B分别在射线OM、ON上移动，△AOB的角平分线AC与BD交于点P. 试问：随着点A、B位置的变化，∠APB的大小是否会变化？若保持不变，请求出∠APB的度数；若发生变化，求出变化范围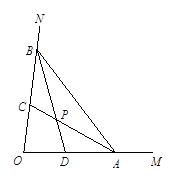
相关试题
，其中
．[
时，求∠BPC的度数. 相关知识点
推荐套卷
（1）如图，∠MON＝80º，点A、B分别在射线OM、ON上移动，△AOB的角平分线AC与BD交于点P. 试问：随着点A、B位置的变化，∠APB的大小是否会变化？若保持不变，请求出∠APB的度数；若发生变化，求出变化范围
粤公网安备 44130202000953号