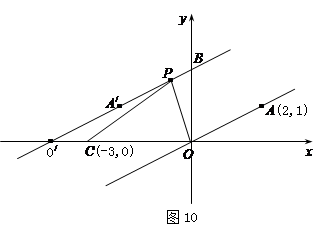已知正比例函数y=kx经过点A(2,1),如图10所示.求这个正比例函数的关系式.
将这个正比例函数的图像向左平移4个单位,写出在这个平移下,点A、原点O的对应点A/、O/的坐标,求出平移后的直线O/A/所对应的函数关系式.
已知点C的坐标为(-3,0),点P(x,y)为线段O/B上一动点(P与O/、B不重合),设△PCO的面积为S.
① 求S与x之间的函数关系式及x的取值范围;
② ② 求当S= 时,点P的坐标.
时,点P的坐标.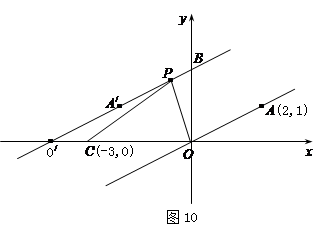
相关知识点
推荐套卷
已知正比例函数y=kx经过点A(2,1),如图10所示.求这个正比例函数的关系式.
将这个正比例函数的图像向左平移4个单位,写出在这个平移下,点A、原点O的对应点A/、O/的坐标,求出平移后的直线O/A/所对应的函数关系式.
已知点C的坐标为(-3,0),点P(x,y)为线段O/B上一动点(P与O/、B不重合),设△PCO的面积为S.
① 求S与x之间的函数关系式及x的取值范围;
② ② 求当S= 时,点P的坐标.
时,点P的坐标.