如图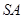 ⊥平面
⊥平面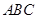 ,
, ⊥
⊥ ,过
,过 做
做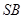
的垂线,垂足为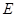 ,过
,过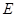 做
做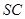 的垂线,垂足为
的垂线,垂足为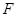 ,求证
,求证 ⊥
⊥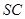 。以下是证明过程:
。以下是证明过程:
要证
 ⊥
⊥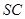
只需证 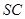 ⊥平面
⊥平面
只需证 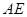 ⊥
⊥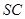 (因为
(因为 ⊥
⊥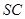 )
)
只需证 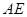 ⊥平面
⊥平面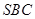
只需证 ① (因为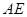 ⊥
⊥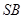 )
)
只需证  ⊥平面
⊥平面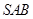
只需证 ② (因为 ⊥
⊥ )
)
由只需证 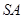 ⊥平面
⊥平面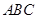 可知上式成立
可知上式成立
所以 ⊥
⊥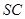
把证明过程补充完整① ② 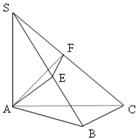
推荐套卷
如图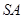 ⊥平面
⊥平面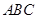 ,
, ⊥
⊥ ,过
,过 做
做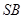
的垂线,垂足为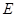 ,过
,过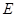 做
做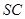 的垂线,垂足为
的垂线,垂足为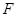 ,求证
,求证 ⊥
⊥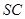 。以下是证明过程:
。以下是证明过程:
要证
 ⊥
⊥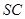
只需证 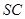 ⊥平面
⊥平面
只需证 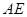 ⊥
⊥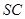 (因为
(因为 ⊥
⊥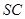 )
)
只需证 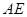 ⊥平面
⊥平面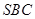
只需证 ① (因为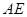 ⊥
⊥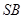 )
)
只需证  ⊥平面
⊥平面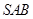
只需证 ② (因为 ⊥
⊥ )
)
由只需证 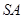 ⊥平面
⊥平面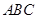 可知上式成立
可知上式成立
所以 ⊥
⊥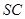
把证明过程补充完整① ② 