某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=-2x+80.设这种产品每天的 销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
(参考关系:销售额=售价×销量,利润=销售额-成本)
相关知识点
推荐套卷

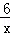 的图象交于A(2,m)、B两点.
的图象交于A(2,m)、B两点.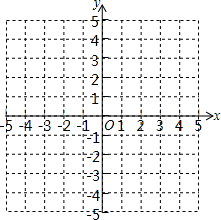
 粤公网安备 44130202000953号
粤公网安备 44130202000953号