不透明的口袋中装有红、黄两种种颜色的小球,从中随机取出一个球,它是红球概率是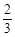 ;往口袋中再放进2个黑球,则取得一个球是红球概率是
;往口袋中再放进2个黑球,则取得一个球是红球概率是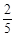 (球除颜色外其余都相同)。
(球除颜色外其余都相同)。
(1)求袋中红球个数;
(2)第一次摸出一个球(不放回),第二次再摸一个,请用画树状图或列表法求两次摸到都是红球概率;
(3)若规定摸到红球得1分,摸到黄球得3分,摸到黑球得5分,小明共摸小球6次(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?
相关知识点
推荐套卷
不透明的口袋中装有红、黄两种种颜色的小球,从中随机取出一个球,它是红球概率是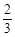 ;往口袋中再放进2个黑球,则取得一个球是红球概率是
;往口袋中再放进2个黑球,则取得一个球是红球概率是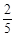 (球除颜色外其余都相同)。
(球除颜色外其余都相同)。
(1)求袋中红球个数;
(2)第一次摸出一个球(不放回),第二次再摸一个,请用画树状图或列表法求两次摸到都是红球概率;
(3)若规定摸到红球得1分,摸到黄球得3分,摸到黑球得5分,小明共摸小球6次(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?