已知函数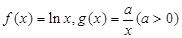 ,设
,设
(1)求 的单调区间;
的单调区间;
(2)若以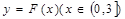 图象上任意一点
图象上任意一点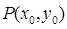 为切点的切线的斜率
为切点的切线的斜率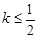 恒成立,求实数的最小值;
恒成立,求实数的最小值;
(3)是否存在实数 ,使得函数
,使得函数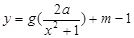 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
推荐套卷
已知函数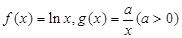 ,设
,设
(1)求 的单调区间;
的单调区间;
(2)若以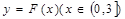 图象上任意一点
图象上任意一点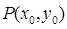 为切点的切线的斜率
为切点的切线的斜率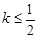 恒成立,求实数的最小值;
恒成立,求实数的最小值;
(3)是否存在实数 ,使得函数
,使得函数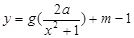 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。