某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为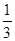
，用ξ表示这5位乘客在第20层下电梯的人数.求：
（1）随机变量ξ的分布列；
（2）随机变量ξ的期望和方差.
相关试题
．
的值；
的值．
，
．
在
上的简图；
，
，求
．
．
，
．
与
的夹角的余弦值；
与
平行，求
的值．
的离心率为
，两焦点之间的距离为4．
于A、B两点．推荐套卷
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为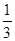，用ξ表示这5位乘客在第20层下电梯的人数.求：
（1）随机变量ξ的分布列；
（2）随机变量ξ的期望和方差.
粤公网安备 44130202000953号