阅读理解:对于二次三项式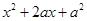 可以直接用公式法分解为
可以直接用公式法分解为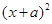 的形式,但对于二次三项式
的形式,但对于二次三项式 ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式 中先加上一项
中先加上一项 ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有 =
= +
+ -
-
= =
= =
= 。
。
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.请用上述方法求出
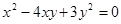 (满足
(满足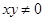 ,且
,且 )中
)中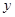 与
与 的关系式。
的关系式。利用上述关系式求
 的值。
的值。
相关知识点
推荐套卷
阅读理解:对于二次三项式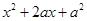 可以直接用公式法分解为
可以直接用公式法分解为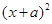 的形式,但对于二次三项式
的形式,但对于二次三项式 ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式 中先加上一项
中先加上一项 ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有 =
= +
+ -
-
= =
= =
= 。
。
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.请用上述方法求出
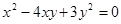 (满足
(满足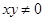 ,且
,且 )中
)中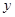 与
与 的关系式。
的关系式。利用上述关系式求
 的值。
的值。