某公司到果园购买某种优质水果,果园对购买3000千克以上(含3000千克)的有两种销售方式,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己运回,已知该公司租车从基地到公司的运输费用是5000元。
(1)分别写出该公司两种购买方案的付款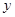 与所购买的水果量
与所购买的水果量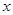 之间的函数关系式;
之间的函数关系式;
(2)当购买量在什么范围时,选择哪种购买方式付款最少?
相关知识点
推荐套卷
某公司到果园购买某种优质水果,果园对购买3000千克以上(含3000千克)的有两种销售方式,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己运回,已知该公司租车从基地到公司的运输费用是5000元。
(1)分别写出该公司两种购买方案的付款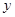 与所购买的水果量
与所购买的水果量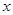 之间的函数关系式;
之间的函数关系式;
(2)当购买量在什么范围时,选择哪种购买方式付款最少?