如图,直角梯形ABMN中,∠NAB=90°，AN∥BM,AB=2,AN=
,BM=
,椭圆C以A,B为焦点且过点N.
（1）建立适当的坐标系,求椭圆C方程;
(2)若点E满足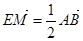
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
是定义在
上的奇函数，且当
时，
．
解集．
．
的值；
，且
，求
的值．
，
．
，求实数
的值；
，求实数
．
；推荐套卷
如图,直角梯形ABMN中,∠NAB=90°，AN∥BM,AB=2,AN=,BM=,椭圆C以A,B为焦点且过点N.
（1）建立适当的坐标系,求椭圆C方程;
(2)若点E满足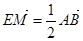,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
粤公网安备 44130202000953号