已知椭圆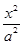
＋
＝1（a>b>0)上的点M (1, 
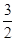)到它的两焦点F1，F2的距离之和为4，A、B分别是它的左顶点和上顶点。
(Ⅰ)求此椭圆的方程及离心率；
(Ⅱ)平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程。
相关试题
在R上单调递减；q：不等式
＞1的解集为R，如果“p或q”为真，且“p且q”为假，求c的取值范围。
,且
,⑴求
的取值范围;⑵求证
;⑶求函数
的取值范围.
,满足f(
)
=f(0),⑴求函数f(x)的最小正周期;⑵求函数f(x)在
上的最大值和最小值.
,最小值为
,求a,b 的
值.推荐套卷
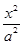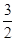已知椭圆＋＝1（a>b>0)上的点M (1, )到它的两焦点F1，F2的距离之和为4，A、B分别是它的左顶点和上顶点。
(Ⅰ)求此椭圆的方程及离心率；
(Ⅱ)平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程。
粤公网安备 44130202000953号