已知抛物线 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线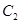 :
: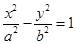 的一个焦点
的一个焦点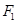 且垂直于
且垂直于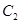 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线 与双曲线
与双曲线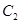 的一个交点是
的一个交点是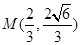 .
.
(Ⅰ)求抛物线 的方程及其焦点
的方程及其焦点 的坐标; (Ⅱ)求双曲线
的坐标; (Ⅱ)求双曲线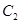 的方程及其离心率
的方程及其离心率 .
.
相关知识点
推荐套卷
已知抛物线 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线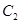 :
: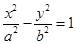 的一个焦点
的一个焦点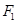 且垂直于
且垂直于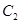 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线 与双曲线
与双曲线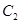 的一个交点是
的一个交点是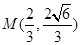 .
.
(Ⅰ)求抛物线 的方程及其焦点
的方程及其焦点 的坐标; (Ⅱ)求双曲线
的坐标; (Ⅱ)求双曲线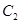 的方程及其离心率
的方程及其离心率 .
.