有两枚大小相同、质地均匀的正四面体玩具，每个玩具的各个面上分别写着数字1，2，3，5. 同时投掷这两枚玩具一次，记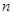
为两个朝下的面上的数字之和.
（Ⅰ）求事件“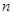不大于6”的概率；
（Ⅱ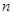）“为奇数”的概率和“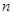为偶数”的概率是不是相等？证明你的结论.
+lg（36－x2）的定义域．
）的定义域、值域，并指出它的周期、奇偶性和单调性
·cos
·tan
；
］
，求f（
）的值.
－α）=－cosα；推荐套卷
有两枚大小相同、质地均匀的正四面体玩具，每个玩具的各个面上分别写着数字1，2，3，5. 同时投掷这两枚玩具一次，记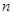为两个朝下的面上的数字之和.
（Ⅰ）求事件“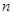不大于6”的概率；
（Ⅱ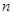）“为奇数”的概率和“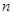为偶数”的概率是不是相等？证明你的结论.
粤公网安备 44130202000953号