设数列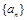 的前
的前 项和为
项和为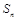 ,且满足
,且满足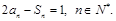
(1)求数列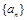 的通项公式;
的通项公式;
(2)在数列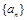 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列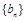 ,在
,在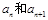 两项之间插入
两项之间插入 个数,使这
个数,使这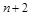 个数构成等差数列,求
个数构成等差数列,求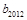 的值;
的值;
(3)对于(2)中的数列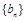 ,若
,若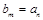 ,并求
,并求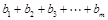 (用
(用 表示).
表示).
推荐套卷
设数列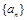 的前
的前 项和为
项和为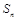 ,且满足
,且满足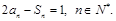
(1)求数列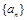 的通项公式;
的通项公式;
(2)在数列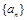 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列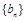 ,在
,在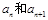 两项之间插入
两项之间插入 个数,使这
个数,使这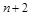 个数构成等差数列,求
个数构成等差数列,求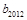 的值;
的值;
(3)对于(2)中的数列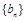 ,若
,若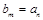 ,并求
,并求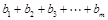 (用
(用 表示).
表示).