如图所示，己知三棱柱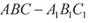
的侧棱与底面垂直，
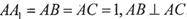，MN分别是
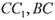的中点，P点在
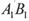上，且满足
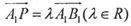
(I)证明：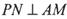
(II)当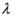
取何值时，直线PN与平面ABC所成的角
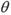最大？并求出该最大角的正切值；
(III) 在（II)条件下求P到平而AMN的距离.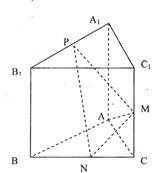
相关试题
，
，其中
为坐标原点.
且
，求向量
与
的夹角；
对任意实数
都成立，求实数
的取值范围.
中，角A、B、C所对的边分别是 a,b,c且a="2," 
的值.
=3，求b,c的值.
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
的表达式（不需证明）；
的最大值为
，
，求
的最小值.
在
上递增，求
的取值范围；
上的存在单调递减区间 ，求推荐套卷
如图所示，己知三棱柱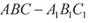的侧棱与底面垂直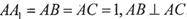，，MN分别是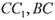的中点，P点在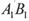上，且满足
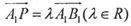
(I)证明：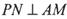
(II)当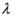取何值时，直线PN与平面ABC所成的角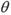最大？并求出该最大角的正切值；
(III) 在（II)条件下求P到平而AMN的距离.
粤公网安备 44130202000953号