在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东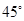
且与点A相距40
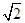海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+
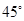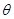(其中sin=
，
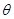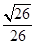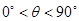)且与点A相距10
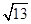海里的位置C.
(1)求该船的行驶速度（单位：海里/小时）;
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.
是奇函数。
，求实数t的取值范围。
对一切实数x恒成立，求实数a的取值范围。
在区间
上的最小值
的表达式。
，
，若
，求实数m的取值范围。
是关于
的方程
的两个实根，且
，求
的值．
是以2为周期的函数，且
时，
，
时，求
的解析式.相关知识点
推荐套卷
在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东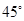且与点A相距40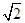海里的位置B，经过40分钟又测得该船已行驶到点A北偏东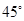+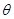(其中sin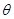=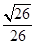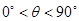，)且与点A相距10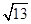海里的位置C.
(1)求该船的行驶速度（单位：海里/小时）;
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.
粤公网安备 44130202000953号