在函数概念的发展过程中，德国数学家狄利克雷（Dirichlet，1805——1859）功不可没。19世纪，狄利克雷定义了一个“奇怪的函数”：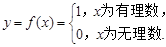
，这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是：（ ）
| A．它没有单调性 | B．它是周期函数，且没有最小正周期 |
| C．它是偶函数 | D．它有函数图像 |
，
，若
，则
的取值范围为（）
时, 函数
和
在同一坐标系内的大致图象是（）
的最小值（ ）
B.
C. 
D.
(
，
，
)的部分图象如图所示，则函数表达式为 （）
，则实数
等于( )
相关知识点
推荐套卷
在函数概念的发展过程中，德国数学家狄利克雷（Dirichlet，1805——1859）功不可没。19世纪，狄利克雷定义了一个“奇怪的函数”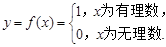：，这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是：（ ）
| A．它没有单调性 | B．它是周期函数，且没有最小正周期 |
| C．它是偶函数 | D．它有函数图像 |
粤公网安备 44130202000953号