如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边向D移动,速度是每秒1厘米,点P从A开始沿AB向B移动,速度是点Q速度的a倍,如果点P,Q分别从A,C同时出发,当其中一点到达终点时运动停止.设运动时间为t秒.已知当t=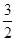 时,四边形APQD是平行四边形.
时,四边形APQD是平行四边形.求a的值;
线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说明理由;
若在某一时刻点P恰好在DQ的垂直平分线上,求此时t的值。
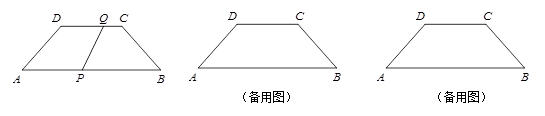
如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边向D移动,速度是每秒1厘米,点P从A开始沿AB向B移动,速度是点Q速度的a倍,如果点P,Q分别从A,C同时出发,当其中一点到达终点时运动停止.设运动时间为t秒.已知当t= 时,四边形APQD是平行四边形.
时,四边形APQD是平行四边形.求a的值;
线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说明理由;
若在某一时刻点P恰好在DQ的垂直平分线上,求此时t的值。
