已知抛物线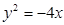 的焦点为F,其准线与x轴交于点
的焦点为F,其准线与x轴交于点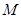 ,过点
,过点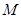 作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与 x轴交于点E(
作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与 x轴交于点E(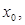 0)。
0)。
(1)求k的取值范围;
(2)求证: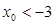 ;
;
(3)△PEF能否成为以EF为底的等腰三角形?若能,求出k的值,若不能,请说明理由。
推荐套卷
已知抛物线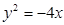 的焦点为F,其准线与x轴交于点
的焦点为F,其准线与x轴交于点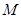 ,过点
,过点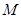 作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与 x轴交于点E(
作斜率为k的直线l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与 x轴交于点E(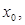 0)。
0)。
(1)求k的取值范围;
(2)求证: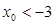 ;
;
(3)△PEF能否成为以EF为底的等腰三角形?若能,求出k的值,若不能,请说明理由。