(本小题满分8分) 
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:≈1.73,
sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
 |
相关知识点
推荐套卷
 中,
中, 平分
平分 且交
且交 边于点
边于点 将
将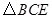 绕点
绕点 顺时针旋转到
顺时针旋转到 的位置,并延长
的位置,并延长 于点
于点 求证:
求证: .
.
 ,其中
,其中 .
. 轴交于点A(-4,0)和B(1,0),与y轴交于C点.
轴交于点A(-4,0)和B(1,0),与y轴交于C点.
 的面积是
的面积是 面积的2倍时,求E点的坐标.
面积的2倍时,求E点的坐标.
 (1)求证:AB=AC;
(1)求证:AB=AC; ,求CE的长.
,求CE的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号