(本大题12分)某镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题: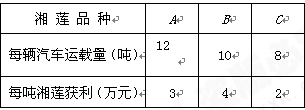
(1)设装运A种湘莲的车辆数为x,装运B种湘莲的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)在(2)的方案中,若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
相关知识点
推荐套卷
 ,计算
,计算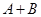 .某同学做此题时误将
.某同学做此题时误将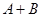 看成了
看成了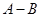 ,求得其结果为
,求得其结果为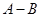 =
=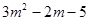 ,若
,若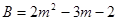 ,请你帮助他求得正确答案.
,请你帮助他求得正确答案.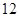 ,
,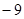 ,
, 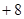 ,
,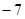 ,+
,+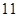 ,
,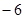 ,
,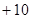 ,
,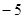
 表示一个人的年龄,用
表示一个人的年龄,用 表示正常情况下的这个人在运动时所能承受的每分钟心跳的最高次数,那么
表示正常情况下的这个人在运动时所能承受的每分钟心跳的最高次数,那么 .
.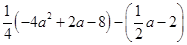 ,其中
,其中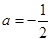
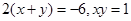 ,求代数式
,求代数式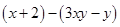 的值
的值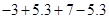
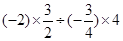
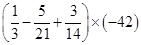
 粤公网安备 44130202000953号
粤公网安备 44130202000953号