如图，直线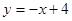
与两坐标轴分别相交于A、B点，点M是线段AB上任意一点（A、B两点除外），过M分别作MC⊥OA于点C，MD⊥OB于D．
 |
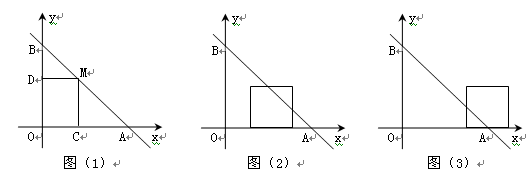（1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化？并说明理由；
（2）当点M运动到什么位置时，四边形OCMD的面积有最大值？最大值是多少？
（3）当四边形OCMD为正方形时，将四边形OCMD沿着x轴的正方向移动，设平移的距离为
，正方形OCMD与△AOB重叠部分的面积为S．试求S与
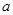的函数关系式并画出该函数的图象．
相关试题
，其中
随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加，据统计，某小区2007年底拥有家庭轿车64辆，2009年底家庭轿
车的拥有量达到100辆，求2007年底到2009年底家庭轿车的拥有量的年平均增长率？(12’)
是一元二次方程
的两个实数根，求实数m的取值范围. (10’)相关知识点
推荐套卷
粤公网安备 44130202000953号