(本小题满分10分）选修4－ 4:坐标系与参数方程
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建极坐标系，已知曲线C: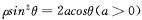
，过点P(－2，－4)的直线l的参数方程为：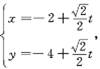
直线l与曲线C分别交于M，N.
(I) 写出曲线C和直线l的普通方程；
(II)若|PM|,|MN|,|PN|成等比数列，求a的值
相关试题
中，角
所对的边分别为
，已知
．
时，
，求
；
，求
的值；
时，若
，求
的光线，经
轴上一点
反射后的射线
过点
．
过点
且与
，求圆
中，
分别为
中点．
平面
；
平面
．
，
是单位圆
上一动点，且点
的中点．
在
轴的正半轴上，求
；
，求点
到直线
的距离．
在
上是增函数，且
.
的取值范围；
在
上的最大值；
，
，求证：
．相关知识点
推荐套卷
(本小题满分10分）选修4－ 4:坐标系与参数方程
在直角坐标系中，以原点为极点，x轴的正半轴为极轴建极坐标系，已知曲线C: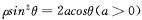，过点P(－2，－4)的直线l的参数方程为：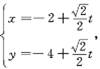
直线l与曲线C分别交于M，N.
(I) 写出曲线C和直线l的普通方程；
(II)若|PM|,|MN|,|PN|成等比数列，求a的值
粤公网安备 44130202000953号