如图为一个平面. 如图1,有1条直线,可把这个平面分成2部分;如图2,有2条直线,可把这个平面最少分成3部分,最多分成4部分;有3条直线,问可以把这个平面分成几部分?请在图3中画出相应的图形.
有4条直线,可把这个平面最少分成 部分,最多分成 部分;
同一平面内
 条直线最少可以把平面分成几部分?最多可以把平面分成几部分?
条直线最少可以把平面分成几部分?最多可以把平面分成几部分?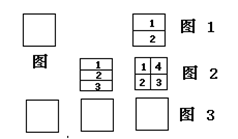
如图为一个平面. 如图1,有1条直线,可把这个平面分成2部分;如图2,有2条直线,可把这个平面最少分成3部分,最多分成4部分;有3条直线,问可以把这个平面分成几部分?请在图3中画出相应的图形.
有4条直线,可把这个平面最少分成 部分,最多分成 部分;
同一平面内
 条直线最少可以把平面分成几部分?最多可以把平面分成几部分?
条直线最少可以把平面分成几部分?最多可以把平面分成几部分?