某玩具厂生产一种儿童智力玩具，每个玩具的材料成本为20元，加工费为t元（t为常数，且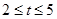
），出厂价为x元
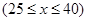，根据市场调查知，日销售量q（单位：个）与
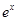成反比，且当每个玩具的出厂价为30元时，日销售量为100个。
（1）求该玩具厂的日利润y元与每个玩具的出厂价x元之间的函数关系式；
（2）若t=5，则每个玩具的出厂价为x为多少元时，该工厂的日利润y最大？并求最大值。
相关试题
中，底面
为矩形，
底面
、
分别是
、
中点．
平面
；
．
：
，直线
交椭圆
两点．
为直径的圆的方程．
中，已知点
，动点
在
轴上的正射影为点
，且满足直线
．
时，求直线
的方程．
中，点
为边
上的点，点
为边
的中点，
，现将
沿
边折至
位置，且平面
平面
．
；
的体积．
的首项为1，前n项和为Sn，且
（
）．
的通项公式；
，
是数列
的前n项和，求
．推荐套卷
某玩具厂生产一种儿童智力玩具，每个玩具的材料成本为20元，加工费为t元（t为常数，且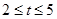），出厂价为x元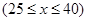，根据市场调查知，日销售量q（单位：个）与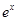成反比，且当每个玩具的出厂价为30元时，日销售量为100个。
（1）求该玩具厂的日利润y元与每个玩具的出厂价x元之间的函数关系式；
（2）若t=5，则每个玩具的出厂价为x为多少元时，该工厂的日利润y最大？并求最大值。
粤公网安备 44130202000953号