问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:

四边形DBFE的面积 ▲ ,
▲ ,
△EFC的面积S1= ▲ ,
△ADE的面积S2= ▲ .
探究发现(2)在(1)中,若
 ,
, ,DE与BC间的距离为
,DE与BC间的距离为 .请证明S2=4S1 S2.
.请证明S2=4S1 S2.
拓展迁移
(3)如图2,平行四边形DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.
相关知识点
推荐套卷
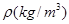 与体积
与体积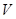
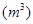 之间的函数关系如图所示,。
之间的函数关系如图所示,。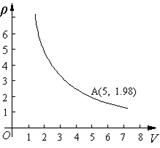
 与
与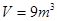 时,二氧化碳的密度
时,二氧化碳的密度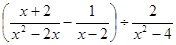 ,请你取一个
,请你取一个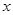 的值,求出此时代数式的值.
的值,求出此时代数式的值. 与
与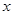 轴的另一个交点为A.过点
轴的另一个交点为A.过点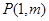 作直线
作直线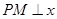 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。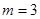 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;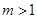 时,连结CA,问
时,连结CA,问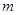 为何值时
为何值时 ?
?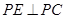 且
且 ,问是否存在
,问是否存在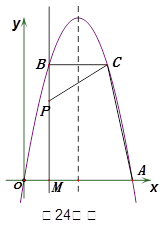
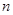 件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排
件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示。设安排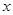 件产品运往A地。
件产品运往A地。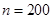 时①根据信息填表:
时①根据信息填表:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号