．设椭圆E: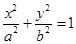 
（a,b>0）过M（2，
） ，N(
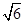,1)两点，O为坐标原点，（I）求椭圆E的方程；
（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。
，求直平行六面体的侧面积．
求证：
．
上一点，左、右焦点分别为F1，F2。
，求
之值。
且椭圆经过
；（2）渐近线方程是
，经过点
。推荐套卷
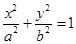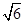．设椭圆E: （a,b>0）过M（2，） ，N(,1)两点，O为坐标原点，（I）求椭圆E的方程；
（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。
粤公网安备 44130202000953号