已知F1(
2，0)，F2(2，0)，点P满足|PF1|－|PF2|＝2，记点P的轨迹为S，过点F2作直线
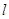与轨迹S交于P、Q两点，过P、Q作直线x＝的垂线PA、QB，垂足分别为A、B，记λ＝|AP|·|BQ|．
（1）求轨迹S的方程；
（2）设点M（1，0），求证：当λ取最小值时，△PMQ的面积为9．
=
,求证：a+
，则
在R上是增函数；
，则
ABC是
；
的最小值为
；
，则A=B；
，则
，
、
，求
的值？推荐套卷
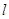已知F1(2，0)，F2(2，0)，点P满足|PF1|－|PF2|＝2，记点P的轨迹为S，过点F2作直线与轨迹S交于P、Q两点，过P、Q作直线x＝的垂线PA、QB，垂足分别为A、B，记λ＝|AP|·|BQ|．
（1）求轨迹S的方程；
（2）设点M（1，0），求证：当λ取最小值时，△PMQ的面积为9．
粤公网安备 44130202000953号