某单位欲招聘一名员工,现有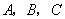 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一
请将表一和图一中的空缺部分补充完整;
竞聘的最后一个程序是由该单位的
 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
况如图二(没有弃权票,每名职工只能推荐一个),请计算每人的得票数;若每票计
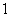 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按 的比例确定
的比例确定
个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
相关知识点
推荐套卷
某单位欲招聘一名员工,现有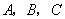 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一
请将表一和图一中的空缺部分补充完整;
竞聘的最后一个程序是由该单位的
 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
况如图二(没有弃权票,每名职工只能推荐一个),请计算每人的得票数;若每票计
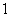 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按 的比例确定
的比例确定
个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.