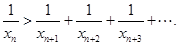过曲线 上的一点
上的一点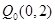 作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线
作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线 ,交x轴于点P3;……如此继续下去得到点列:
,交x轴于点P3;……如此继续下去得到点列: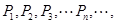 设
设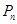 的横坐标为
的横坐标为
(I)试用n表示 ;
;
(II)证明: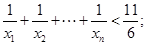
(III)证明: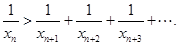
推荐套卷
过曲线 上的一点
上的一点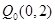 作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线
作曲线的切线,交x轴于点P1,过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线,交x轴于点P2;过P2作垂直于x轴的直线交曲线于Q2,过Q2作曲线的切线 ,交x轴于点P3;……如此继续下去得到点列:
,交x轴于点P3;……如此继续下去得到点列: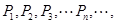 设
设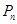 的横坐标为
的横坐标为
(I)试用n表示 ;
;
(II)证明: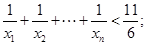
(III)证明: