某公司有电子产品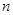 件,合格率为96%,在投放市场之前
件,合格率为96%,在投放市场之前 ,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行
,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行 ,即把
,即把 件打成一包,对这
件打成一包,对这 件产品进行一次性整体检验,如果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
件产品进行一次性整体检验,如果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了 次
次
(1)探求检测这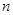 件产品的检测次数
件产品的检测次数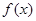 ;
;
(2)如果设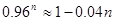 ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品?
推荐套卷
某公司有电子产品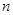 件,合格率为96%,在投放市场之前
件,合格率为96%,在投放市场之前 ,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行
,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行 ,即把
,即把 件打成一包,对这
件打成一包,对这 件产品进行一次性整体检验,如果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
件产品进行一次性整体检验,如果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了 次
次
(1)探求检测这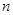 件产品的检测次数
件产品的检测次数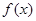 ;
;
(2)如果设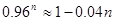 ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品?