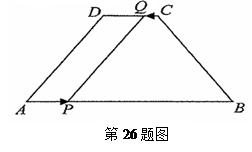
(本题8分)如图,在梯形ABCD中,AB∥DC,AB=14cm,CD=6cm.点P从点A出发,以2cm/s的速度沿AB向终点B运动;点Q从点C出发,以1cm/s的速度沿CD向终点D运动(P、Q两点中,有一个点运动到终点时,所有运动即终止),设P、Q同时出发并运动了t秒。
(1)当DQ=AP时,四边形APQD是平形四边形,求出此时t的值;
(2) 试问在这样的运动过程中,是否存在某一时刻,使梯形PBCQ的面积是梯形ABCD面积的一半?若存在,求出这样的t的值,若不存在,请说明理由。
 |
推荐套卷
 的图象如图所示:请根据图象回答:
的图象如图所示:请根据图象回答: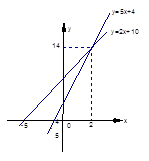
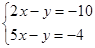 的解为_____。
的解为_____。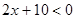 的解集为_____。
的解集为_____。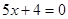 的解为_____。
的解为_____。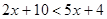 的解集为_____。
的解集为_____。
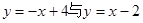 的图象,并利用图象解答下列问题:
的图象,并利用图象解答下列问题: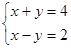 ;(3)不等式
;(3)不等式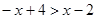
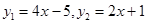 ,请回答下列问题:
,请回答下列问题: 的值等于0?
的值等于0?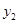 的值恒小于0?
的值恒小于0? 粤公网安备 44130202000953号
粤公网安备 44130202000953号