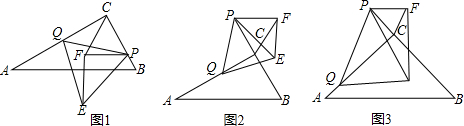
已知A(2,0),直线y=(2−)x−2交x轴于点F,y轴于点B,直线l∥AB且交 y轴于点C,交x轴于点D,点A关于直线l的对称点为A' ,连结AA',A'D。直线l从AB开始,以1个单位每秒的速度沿y轴正方向向上平移,设移动时间为t.求A'点的坐标(用t的代数式表示)
请猜想AB与AF长度的数量关系,并说明理由
过点C作直线AB的垂线交直线y=(2−)x−2于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?

相关知识点
推荐套卷
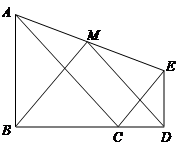
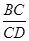 ;
;
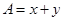 ,其中
,其中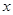 可取
可取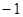 、2,
、2,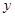 可取
可取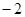 、3.试求
、3.试求 是正值的概率.
是正值的概率.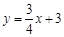 的图像与y轴交于点A,点M在正比例函数
的图像与y轴交于点A,点M在正比例函数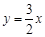 的图像上,且MO=MA.求点M的坐标.
的图像上,且MO=MA.求点M的坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号