如图,已知:AC⊥AB,BD⊥AB,且AC=BE,AE=BD,求证:△CDE是等腰直角三角形;
证明:∵AC⊥AB,BD⊥AB ∴∠CAE=∠DBE=90°
∵AC= BE,AE=BD ∴△ACE≌△BED
∴CE=DE且∠ACE=∠BED
∵∠ACE+∠AEC=90° ∴∠AEC+∠BED=90°
∴∠CED=90° ∴△CED为等腰直角三角形
利用上题的解题思路解答下列问题:
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.若BD=AC,AE=CD,在下图中画出符合题意的图形,求出∠APE的度数;
若AC=BD,CD=AE,则∠APE=__________°
相关知识点
推荐套卷
 ,
,

 _______________;(3分)
_______________;(3分) ______________;(4分)
______________;(4分)

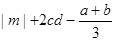 的值.(5分)
的值.(5分) 粤公网安备 44130202000953号
粤公网安备 44130202000953号