已知椭圆C: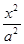 +
+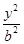 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+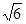 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(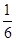 ,0)求实数k的取值范围。
,0)求实数k的取值范围。
推荐套卷
已知椭圆C: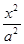 +
+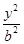 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+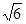 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(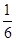 ,0)求实数k的取值范围。
,0)求实数k的取值范围。