（本小题满分12分）
某校为宣传县教育局提出的“教育发展，我的责任”教育实践活动，要举行一次以“我
为教育发展做什么”为主题的的演讲比赛，比赛分为初赛、复赛、决赛三个阶段进行，已知
某选手通过初赛、复赛、决赛的概率分别是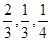
，且各阶段通过与否相互独立.
（I）求该选手在复赛阶段被淘汰的概率；
（II）设该选手在比赛中比赛的次数为
，求的分布列、数学期望和方差.
相关试题
，
的单调区间；
内的最小值为
，求
的值.（参考数据
）
为等比数列，其前
项和为
，已知
，且
，
，
成等差，
（
），记
，若
对于
恒成立，求实数
的取值范围.
，
时，求
的值；
在
上的值域.
中，
， 
的大小；
时，求
为函数
的定义域，集合
.
；
的取值范围.推荐套卷
（本小题满分12分）
某校为宣传县教育局提出的“教育发展，我的责任”教育实践活动，要举行一次以“我
为教育发展做什么”为主题的的演讲比赛，比赛分为初赛、复赛、决赛三个阶段进行，已知
某选手通过初赛、复赛、决赛的概率分别是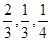，且各阶段通过与否相互独立.
（I）求该选手在复赛阶段被淘汰的概率；
（II）设该选手在比赛中比赛的次数为，求的分布列、数学期望和方差.
粤公网安备 44130202000953号