(本小题满分14分)已知定义在实数集上的函数 N
N ,其导函数记为
,其导函数记为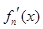 ,且满足
,且满足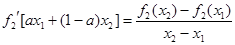 ,其中
,其中 、
、 、
、 为常数,
为常数,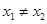 .设函数
.设函数
 R且
R且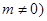 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数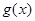 无极值点,其导函数
无极值点,其导函数 有零点,求m的值;
有零点,求m的值;
(Ⅲ)求函数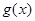 在
在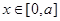 的图象上任一点处的切线斜率k的最大值.
的图象上任一点处的切线斜率k的最大值.
推荐套卷
(本小题满分14分)已知定义在实数集上的函数 N
N ,其导函数记为
,其导函数记为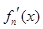 ,且满足
,且满足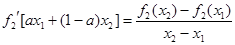 ,其中
,其中 、
、 、
、 为常数,
为常数,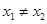 .设函数
.设函数
 R且
R且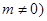 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数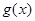 无极值点,其导函数
无极值点,其导函数 有零点,求m的值;
有零点,求m的值;
(Ⅲ)求函数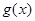 在
在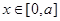 的图象上任一点处的切线斜率k的最大值.
的图象上任一点处的切线斜率k的最大值.