已知：关于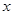
的一元二次方程
（m为实数）若方程有两个不相等的实数根，求
的取值范围；在（1）的条件下，求证：无论
取何值，抛物线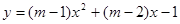
总过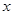轴上的一个固定点；若
是整数，且关于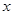的一元二次方程有两个不相等的整数根，把抛物线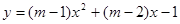向右平移3个单位长度，求平移后的解析式．
，
时，
；
时，
。
时，求y的值。
的所有整数解的和。
（在数轴上把解集表示出来）
相关知识点
推荐套卷
已知：关于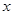的一元二次方程（m为实数）若方程有两个不相等的实数根，求
的取值范围；在（1）的条件下，求证：无论
取何值，抛物线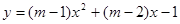总过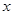轴上的一个固定点；若
是整数，且关于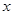的一元二次方程有两个不相等的整数根，把抛物线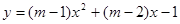向右平移3个单位长度，求平移后的解析式．
粤公网安备 44130202000953号