设二次函数f(x)=mx2+nx+t的图像过原点,g(x)=ax3+bx−3(x>0),f(x), g(x)的导函数为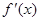 ,g¢(x),且
,g¢(x),且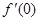 ="0,"
="0,"  =−2,f(1)="g(1),"
=−2,f(1)="g(1)," 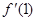 =g¢(1).
=g¢(1).
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)−g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.
相关知识点
推荐套卷
设二次函数f(x)=mx2+nx+t的图像过原点,g(x)=ax3+bx−3(x>0),f(x), g(x)的导函数为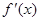 ,g¢(x),且
,g¢(x),且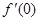 ="0,"
="0,"  =−2,f(1)="g(1),"
=−2,f(1)="g(1)," 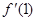 =g¢(1).
=g¢(1).
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)求F(x)=f(x)−g(x)的极小值;
(Ⅲ)是否存在实常数k和m,使得f(x)³kx+m和g(x)£kx+m成立?若存在,求出k和m的值;若不存在,说明理由.