如图，已知点C为AB上的一点，AC＝12㎝，CB＝
AC，D、E分别为AC、AB的中点，求DE的长．
 |
相关试题
2＝2二次函数y=ax²-6ax+c（a＞0）的图像抛物线过点C（0,4），设抛物线的顶点为D。
（1）若抛物线经过点（1，-6），求二次函数的解析式；
（2）若a=1时，试判断抛物线与x轴交点的个数；
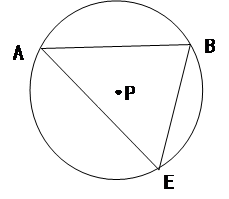
（3）如图所示A、B是⊙P上两点，AB=8，AP=5。且抛物线过点A(x1,y1),B(x2,y2),并有AD=BD。设⊙P上一动点E（不与A、B重合），且∠AEB为锐角，若＜a≤1时，请判断∠AEB与∠ADB的大小关系，并说明理由。
如图，点C在以AB为直径的半圆O上，以点A为旋转中心，以∠β（0°＜β＜90°）为旋转角度将B旋转到点D，过点D作DE⊥AB于点E，交AC于点F，过点C作圆O的切线交DE于点G。
（1）求证：∠GCA=∠OCB；
（2）设∠ABC=m°，求∠DFC的值；
（3）当G为DF的中点时，请探究∠β与∠ABC的关系，并说明理由。
已知抛物线y=x²-4x+3．
（1）该抛物线的对称轴是 ，顶点坐标 ；
（2）将该抛物线向上平移2个单位长度，再向左平移3个单位长度得到新的二次函数图像，请写出相应的解析式，并用列表，描点，连线的方法画出新二次函数的图像；
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
（3）新图像上两点A（x1，y1），B（x2，y2），它们的横坐标满足＜-2，且-1＜＜0，试比较y1，y2，0三者的大小关系．
粤公网安备 44130202000953号