已知抛物线D的顶点是椭圆Q：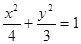
的中心O，焦点与椭圆Q的右焦点重合，点
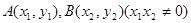是抛物线D上的两个动点，且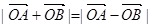
（1）求抛物线D的方程及y1y2的值；
（2）求线段AB中点轨迹E的方程；
（3）在曲线E上寻找一点，使得该点与直线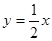
的距离最近.
相关试题
.
在
和
处的切线互相平行，求
的值；
的单调区间；
，若对任意
，均存在
，使得
，求
,椭圆
以
的长轴为短轴,且与
,求直线
的方程.
的前
项和
，数列
满足
．
；（Ⅱ）求数列
；
，求数列
的前
．
在
及
时取得极值．
，都有
成立，求c的取值范围．
（
）的右焦点为
，离心率为
.
，求椭圆的方程；
与椭圆相交于
，
两点，
分别为线段
的中点. 若坐标原点
在以
为直径的圆上，且
，求
的取值范围.推荐套卷
已知抛物线D的顶点是椭圆Q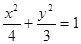：的中心O，焦点与椭圆Q的右焦点重合，点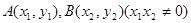是抛物线D上的两个动点，且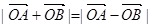
（1）求抛物线D的方程及y1y2的值；
（2）求线段AB中点轨迹E的方程；
（3）在曲线E上寻找一点，使得该点与直线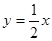的距离最近.
粤公网安备 44130202000953号