(本小题满分16分)某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 (
( )千元.设该容器的建造费用为
)千元.设该容器的建造费用为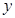 千元.
千元.
(1)写出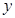 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的 .
.
推荐套卷
(本小题满分16分)某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 (
( )千元.设该容器的建造费用为
)千元.设该容器的建造费用为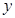 千元.
千元.
(1)写出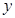 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的 .
.