对于抛物线 .
.(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;
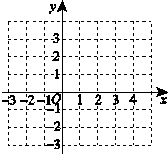
(3)利用以上信息解答下列问题:若关于x的一元二次方程
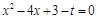 (t为实数)在
(t为实数)在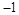 <x<
<x<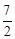 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .
对于抛物线 .
.(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线;

(3)利用以上信息解答下列问题:若关于x的一元二次方程
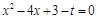 (t为实数)在
(t为实数)在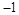 <x<
<x<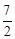 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .