（本小题满分12分）
如图，在Rt△OAB中，∠OAB＝90°，且点B的坐标为（4，2）．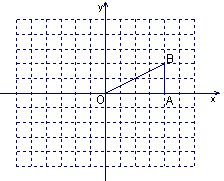
⑴ 画出
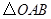关于点O成中心对称的
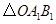，并写出点B1的坐标；⑵ 求出以点B1为顶点，并经过点B的二次函数关系式．
相关试题
如图，在四边形ABCD中，DC∥AB，BD平分∠ADC，∠ADC=60°，过点B作BE⊥DC，过点A作AF⊥BD，垂足分别为E、F，连接EF判断△BEF的形状，并说明理由
＝4，则
的值为多少?
于点
,
平分交
于点
，
于点
，求
的度数 
相关知识点
推荐套卷
（本小题满分12分）
如图，在Rt△OAB中，∠OAB＝90°，且点B的坐标为（4，2）．⑴ 画出
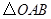关于点O成中心对称的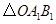，并写出点B1的坐标；⑵ 求出以点B1为顶点，并经过点B的二次函数关系式．
如图，在四边形ABCD中，DC∥AB，BD平分∠ADC，∠ADC=60°，过点B作BE⊥DC，过点A作AF⊥BD，垂足分别为E、F，连接EF判断△BEF的形状，并说明理由
粤公网安备 44130202000953号