(第(1)题4分、第(2)题5分,共9分)(1) 计算:

 +
+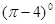
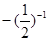 .
. (2)抛物线
 的部分图象如图所示,
的部分图象如图所示,
①求出函数解析式;
②写出与图象相关的2个正确结论:
(对称轴方程,图象与x正半轴、y轴交点坐标例外)
相关知识点
推荐套卷
(第(1)题4分、第(2)题5分,共9分)(1) 计算:

 +
+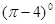
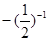 .
. (2)抛物线
 的部分图象如图所示,
的部分图象如图所示,
①求出函数解析式;
②写出与图象相关的2个正确结论:
(对称轴方程,图象与x正半轴、y轴交点坐标例外)