如右图,在平面直角坐标系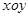 中,已知“葫芦”曲线
中,已知“葫芦”曲线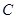 由圆弧
由圆弧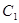 与圆弧
与圆弧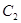 相接而成,两相接点
相接而成,两相接点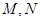 均在直线
均在直线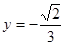 上.圆弧
上.圆弧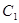 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点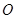 ,半径为
,半径为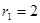 ;圆弧
;圆弧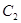 过点
过点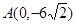 .
.
(I)求圆弧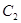 的方程;
的方程;
(II)已知直线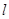 :
: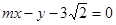 与“葫芦”曲线
与“葫芦”曲线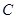 交于
交于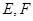 两点.当
两点.当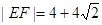 时,求直线
时,求直线 的方程.
的方程.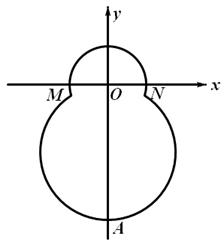
相关知识点
推荐套卷
如右图,在平面直角坐标系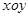 中,已知“葫芦”曲线
中,已知“葫芦”曲线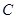 由圆弧
由圆弧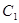 与圆弧
与圆弧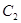 相接而成,两相接点
相接而成,两相接点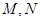 均在直线
均在直线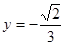 上.圆弧
上.圆弧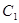 所在圆的圆心是坐标原点
所在圆的圆心是坐标原点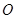 ,半径为
,半径为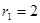 ;圆弧
;圆弧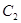 过点
过点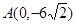 .
.
(I)求圆弧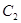 的方程;
的方程;
(II)已知直线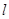 :
: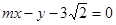 与“葫芦”曲线
与“葫芦”曲线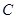 交于
交于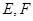 两点.当
两点.当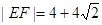 时,求直线
时,求直线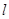 的方程.
的方程.