如图,FD垂直于矩形ABCD所在平面,CE//DF,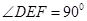 .
.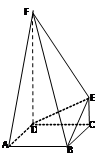
(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB =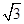 ,EF =
,EF =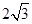 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
相关知识点
推荐套卷
如图,FD垂直于矩形ABCD所在平面,CE//DF,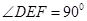 .
.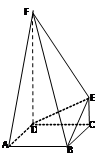
(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB =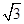 ,EF =
,EF =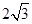 ,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?
,则另一边BC的长为何值时,二面角B-EF-D的大小为45°?