（已知抛物线C:y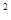
=4x，F是C的焦点，过焦点F的直线l与C交于 A，B两点，O为坐标原点。
（1）求
·
的值；（2）设
=
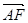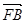，求△ABO的面积S的最小值；
（3）在（2）的条件下若S≤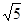
，求的取值范围。
相关试题
满足
. 
上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB//OP，
,求椭圆的方程
=x+ax2+blnx，曲线y=
≤2x-2．
是圆
上的动点，
的取值范围；
恒成立，求实数
的取值范围。
相关知识点
推荐套卷
（已知抛物线C:y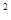=4x，F是C的焦点，过焦点F的直线l与C交于 A，B两点，O为坐标原点。
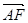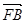（1）求·的值；（2）设=，求△ABO的面积S的最小值；
（3）在（2）的条件下若S≤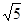，求的取值范围。
粤公网安备 44130202000953号